We have a working paper out on a new way of modelling the relationship between emissions and GDP per capita, a literature that has been dominated for more than two decades by the environmental Kuznets curve (EKC) approach. I presented an early version of this paper at the AARES conference at Port Macquarie in February. I will also be presenting it at the 6th Atlantic Workshop in A Toxa, Spain in late June and then at the World Congress of Environmental and Resource Economics in Istanbul a few days later.
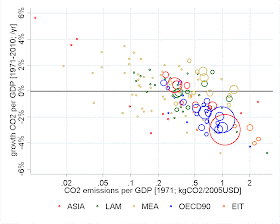
The paper emerged from our work on Chapter 5 of the recently released Working Group III volume of the IPCC 5th Assessment Report. Reyer Gerlagh, who was one of the coordinating lead authors on my chapter drew up a version of the following graph and asked me if it would be suitable for the section I was writing on economic growth and emissions:
I liked this graph so much that I said we should write a paper about it, which we have now completed. Rather than compare the levels of emissions and GDP per capita as is usually done in the EKC literature, the graph compares the average growth rates of these two variables over a 40 year period (1971-2010). We can see that faster economic growth is associated with faster carbon emissions growth but that there is also a lot of variation around this main trend in the data. The further "southeast" a bubble is, the faster emissions per dollar of GDP (emissions intensity) declined in that country. As you can see China (the big red circle) and the US the big blue circle both had rapid declines in emissions intensity. But emissions intensity also rose in many countries and it is not immediately obvious how it relates to development status.*
One of the nice things about using growth rates rather than levels of variables is that it avoids several econometric problems that have plagued this literature. First and foremost is the issue of unit roots and non-linear functions of unit roots raised by Martin Wagner. Differencing the variables removes that issue, but using long-run growth rates focuses attention on long-run behavior, whereas using first differences would focus on the short-run. Then there is the issue of time effects raised by Vollebergh et al. We think our approach does a good job there too. The constant in a regression of emissions growth rates on income growth rates represents the rate of emissions growth if there were no economic growth. We think this is a good definition of a time effect. The paper discusses further econometric issues.
The other nice thing about using growth rates is that we can test the three main leading approaches to modelling the emissions-income relationship in a single framework:
In this equation all variables are in logs and "hats" (or more elegantly circumflex accents) indicate growth rates. On the lefthand side is the emissions per capita growth rate. As mentioned above the constant, alpha, represents the time effect. G-hat is the growth rate of GDP capita. The estimate of beta(1), therefore, tests the IPAT theory that growth causes increases in impacts. The term beta(2)*G(i) tests the EKC theory. This is because if beta(2) is negative then beyond a certain income level (the "turning point") more growth reduces emissions rather than increases emissions. The other main approach to modelling emissions growth has been the convergence approach, including the Green Solow Model of Brock and Taylor. We test this with the fourth term in the regression, which is the level of emissions intensity in the first year of the sample. If delta is negative, then countries with high initial emissions intensities saw more rapid decline in emissions. We also test for any effect of the level of GDP (gamma*G(i)) and for various other exogenous variables including fossil fuel endowments, legal origin, and climate.
It turns out that for both carbon and sulfur dioxide the effect of growth is very significant and close to a one to one effect. For sulfur there is a significant time effect - emissions fell by about 1.2% a year for a typical country when there was no economic growth. The convergence effect is also highly significant and probably explains a lot of the reduction in emissions intensity in both China and the US. But there is no environmental Kuznets curve effect in the full sample estimates.** While there is a marginally significant coefficient for one dataset, all the turning points are far out of sample and insignificant.
The environmental Kuznets curve has become so iconic that it often appears in introductory environmental economics textbooks. It probably is valid as a stylized fact for urban air pollution concentrations but it's not a good model of emissions of either carbon dioxide or sulfur emissions. We're hoping that the figure of the growth effect above and this one of emissions convergence:
might replace it.
* The blue circles are the developed countries that were members of the OECD in 1990. Orange is "economies in transition" - Eastern Europe and the former Soviet Union. The other colors are the developing regions in Asia, Latin America, and the Middle East and North Africa.
** When we split the sample into two periods we find a very significant coefficient for sulfur in the second period, but the turning point is at $38k and is not statistically significant.
The paper emerged from our work on Chapter 5 of the recently released Working Group III volume of the IPCC 5th Assessment Report. Reyer Gerlagh, who was one of the coordinating lead authors on my chapter drew up a version of the following graph and asked me if it would be suitable for the section I was writing on economic growth and emissions:
I liked this graph so much that I said we should write a paper about it, which we have now completed. Rather than compare the levels of emissions and GDP per capita as is usually done in the EKC literature, the graph compares the average growth rates of these two variables over a 40 year period (1971-2010). We can see that faster economic growth is associated with faster carbon emissions growth but that there is also a lot of variation around this main trend in the data. The further "southeast" a bubble is, the faster emissions per dollar of GDP (emissions intensity) declined in that country. As you can see China (the big red circle) and the US the big blue circle both had rapid declines in emissions intensity. But emissions intensity also rose in many countries and it is not immediately obvious how it relates to development status.*
One of the nice things about using growth rates rather than levels of variables is that it avoids several econometric problems that have plagued this literature. First and foremost is the issue of unit roots and non-linear functions of unit roots raised by Martin Wagner. Differencing the variables removes that issue, but using long-run growth rates focuses attention on long-run behavior, whereas using first differences would focus on the short-run. Then there is the issue of time effects raised by Vollebergh et al. We think our approach does a good job there too. The constant in a regression of emissions growth rates on income growth rates represents the rate of emissions growth if there were no economic growth. We think this is a good definition of a time effect. The paper discusses further econometric issues.
The other nice thing about using growth rates is that we can test the three main leading approaches to modelling the emissions-income relationship in a single framework:
In this equation all variables are in logs and "hats" (or more elegantly circumflex accents) indicate growth rates. On the lefthand side is the emissions per capita growth rate. As mentioned above the constant, alpha, represents the time effect. G-hat is the growth rate of GDP capita. The estimate of beta(1), therefore, tests the IPAT theory that growth causes increases in impacts. The term beta(2)*G(i) tests the EKC theory. This is because if beta(2) is negative then beyond a certain income level (the "turning point") more growth reduces emissions rather than increases emissions. The other main approach to modelling emissions growth has been the convergence approach, including the Green Solow Model of Brock and Taylor. We test this with the fourth term in the regression, which is the level of emissions intensity in the first year of the sample. If delta is negative, then countries with high initial emissions intensities saw more rapid decline in emissions. We also test for any effect of the level of GDP (gamma*G(i)) and for various other exogenous variables including fossil fuel endowments, legal origin, and climate.
It turns out that for both carbon and sulfur dioxide the effect of growth is very significant and close to a one to one effect. For sulfur there is a significant time effect - emissions fell by about 1.2% a year for a typical country when there was no economic growth. The convergence effect is also highly significant and probably explains a lot of the reduction in emissions intensity in both China and the US. But there is no environmental Kuznets curve effect in the full sample estimates.** While there is a marginally significant coefficient for one dataset, all the turning points are far out of sample and insignificant.
The environmental Kuznets curve has become so iconic that it often appears in introductory environmental economics textbooks. It probably is valid as a stylized fact for urban air pollution concentrations but it's not a good model of emissions of either carbon dioxide or sulfur emissions. We're hoping that the figure of the growth effect above and this one of emissions convergence:
might replace it.
* The blue circles are the developed countries that were members of the OECD in 1990. Orange is "economies in transition" - Eastern Europe and the former Soviet Union. The other colors are the developing regions in Asia, Latin America, and the Middle East and North Africa.
** When we split the sample into two periods we find a very significant coefficient for sulfur in the second period, but the turning point is at $38k and is not statistically significant.

No comments:
Post a Comment